Atalanta is a figure from Greek mythology known for her speed and prowess as a huntress. She was one of the Argonauts, joining Jason and the crew in their quest for the Golden Fleece. She is a symbol of feminine strength, independence, and determination.

Hippomenes fell in love with Atalanta and sought to marry her. She would only marry him if he could outrun her; otherwise he would be put to death. To win the race he sought help from the goddess Aphrodite, who gave him three golden apples. During the race, Atalanta was distracted by the golden fruit and stopped to pick them up. By the time she gathered all three, Hippomenes had surged ahead and won the race. Bound by her vow, she married Hippomenes.
Suppose Atalanta had not been distracted by the apples. In order for the two runners to reach the final destination, they must first reach a halfway point. Then, to reach the next point, they must cover half of the remaining distance, and so on, creating an infinite series of distances to cover. This suggests that reaching the destination involves an infinite number of steps. In such a case, who would win?

Now we come to Achilles, a prominent figure in Greek mythology, considered one of the greatest warriors of the Trojan War. Suppose Achilles, also known for his incredible speed, engages in a footrace with a mythical tortoise. To make the race fair, Achilles gives the tortoise a head start. If the tortoise is given a head start and Achilles is to catch up, he must first reach the point where the tortoise started. However, by the time Achilles reaches that starting point, the tortoise has moved forward to another point. Now, Achilles must reach this new point where the tortoise was, but in that time, the tortoise has moved forward again. According to this reasoning, Achilles would continually have to reach the point where the tortoise was, but by the time he gets there, the tortoise will have moved ahead, creating an infinite series of distances for Achilles to cover and making it impossible for him to overtake the tortoise.
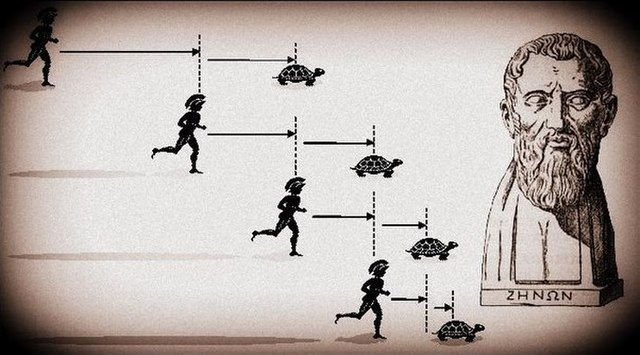
Zeno of Elea was a philosopher who lived in the 5th century BCE, and was a prominent figure in the Eleatic school of thought. He is famous for his paradoxes that challenged ideas about motion, space, and infinity. The examples above illustrate Zeno's Paradox by examining how an infinite division of distance can make it impossible for Achilles to overtake the tortoise or for Atalanta to complete the race, even without the sparkly apples.
Much like how Zeno's paradox suggests an infinite number of steps to reach a destination, a career path might seem to involve an endless succession of smaller achievements, learning curves, or advancements before arriving at a desired position or career milestone. It might seem like you're taking all these steps but getting nowhere. However, just as motion in the real world doesn't adhere to the paradox, actual career progress is tangible and achievable. While the journey might seem like an endless set of hurdles, individuals can progress by focusing on and accomplishing one step at a time, ultimately moving closer to their career aspirations. As long as you are not distracted by shiny apples, or preoccupied with things that seem just out of reach, you will succeed.
It took centuries to mathematically disprove Zeno, but Aristotle successfully challenged Zeno's premise:
Zeno’s reasoning, however, is fallacious, when he says that if everything when it occupies an equal space is at rest, and if that which is in locomotion is always in a now, the flying arrow is therefore motionless. This is false; for time is not composed of indivisible nows any more than any other magnitude is composed of indivisibles.*
Hopefully this is not all Greek to you. All you really need to know from Atalanta and Achilles is to keep at it and you will succeed.
*The complete works of Aristotle: The revised Oxford Translation. Ed. Jonathan Barnes. Vol. 1, Physics. Princeton University Press, 1984. p. 110.